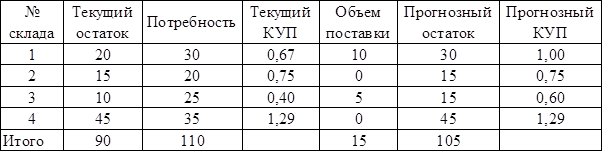Методика распределения различных ресурсов предприятия на основе анализа потребностей клиента

3) Определение значения для текущего цикла расчета:

, (2.47)

где – суммарный заказ на все склады (количество ресурса, которое необходимо распределить).

4) Проверка достижения заданной степени точности ():

, (2.48)

где – значения коэффициента удовлетворения потребности соответственно n-го и n–1-го цикла подбора.

Если условие 2.48 верно, то следующим шагом выполняется вторая операция с использованием в расчете значения полученного на третьем этапе последнего цикла подбора. В противном случае необходимо перейти к пятому пункту алгоритма.

5) Расчет размера заказа по формуле 2.33 с использованием значения , полученного на третьем этапе последнего цикла подбора.

Первоначальное оптимальное значение задается любое. Чем ближе первоначальное значение будет к оптимальному, тем меньше циклов пересчета потребуется для расчета оптимального значения . Мы использовали для первого значения , равный единице.

После расчета оптимального значения заданной степени точности по формуле 2.33 мы рассчитываем объем поставки ресурса на каждый склад. Для приведенного примера равен 1,2. В результате проведенного распределения структура запасов выравнивается, за исключением четвертого склада. На текущий момент нет возможности выровнять остаток по этому складу на оптимальное значение , но при систематической работе по предложенной методике ситуация нормализуется и на нем.

Теперь решим ту же задачу, но с необходимостью распределить между четырьмя складами 15 единиц ресурса.

Таблица 2.7

Пример № 2 распределения ресурсов с использованием

Оптимизируя структуру остатков в процессе распределения ресурса, удается вывести значение на 0,8. Это говорит о том, что при равномерном удовлетворении потребности каждого склада в рассматриваемом виде блага, дефицит будет покрыт только на 80 %. Такое решение не всегда является оптимальным для предпринимателя. Не все склады могут иметь одинаковую значимость для бизнеса в целом. Ранжирование по важности может осуществляться с использованием различных признаков, это может быть объем продаж, доля в выручке, рентабельность, выгодность расположения и т.д. В качестве примера для ранжирования используем значение Потребности. Тогда получаем следующий порядок важности складов: № 4; № 1; № 3; № 2. За оптимальное примем 100 % покрытие потребности. Тогда с использованием формулы 2.33 задача будет иметь следующее решение:

Таблица 2.8

Пример № 3 распределения ресурсов с использованием